William Blake e lo spaziotempo

Auguries of Innocence – William Blake
To see a World in a Grain of Sand
And a Heaven in a Wild Flower
Hold Infinity in the palm of your hand
And Eternity in an hour.

Questo è l’inizio di una poesia meravigliosa di Blake, che potrebbe essere tradotto più o meno così:

Per vedere un mondo in un granello di sabbia,
E un paradiso in un fiore di campo,
Poni l’infinito nel palmo della mano
E l’eternità in un’ora.

Il bello è che non l’ho trovata in un libro di storia della letteratura, ma in un libro di fisica, “La danza dei maestri Wu Li”, che tanto per cambiare tratta di fisica moderna, quantistica e relatività.

In questo specifico caso, il tema è lo spaziotempo. L’introduzione dello spaziotempo in fisica, per merito di Einstein, è stata una rivoluzione molto più grande di quanto possa apparire a prima vista. Il motivo principale è che per la prima volta Einstein dimostrò matematicamente qualcosa che non poteva essere comprovato da una esperienza diretta. E l’esperienza diretta è la base della fisica Newtoniana. Avventurandosi quindi nel mondo dell’astrazione pura, fisica e poesia si avvicinano sino a toccarsi, e questo è il punto di contatto tra Blake e Einstein.

Noi non riusciamo a immaginare un continuum spaziotemporale, perché i nostri sensi ci rimandano un mondo tridimensionale in cui il tempo è una variabile “assoluta”, che scorre solo in avanti. E NON E’ POSSIBILE immaginarlo. Non lo è come non sarebbe possibile a chi vive in un mondo a due dimensioni (un piano) immaginare un solido tridimensionale.

Ma. Ma come sempre c’è un ma, perché l’umanità è ricca di persone piene di immaginazione. E quindi un giorno è arrivato Guy Murchie, che ha scritto il libro “Music of Spheres”, all’interno del quale c’è l’illustrazione che ho riprodotto con pazienza visto che in rete non ne ho trovato traccia.

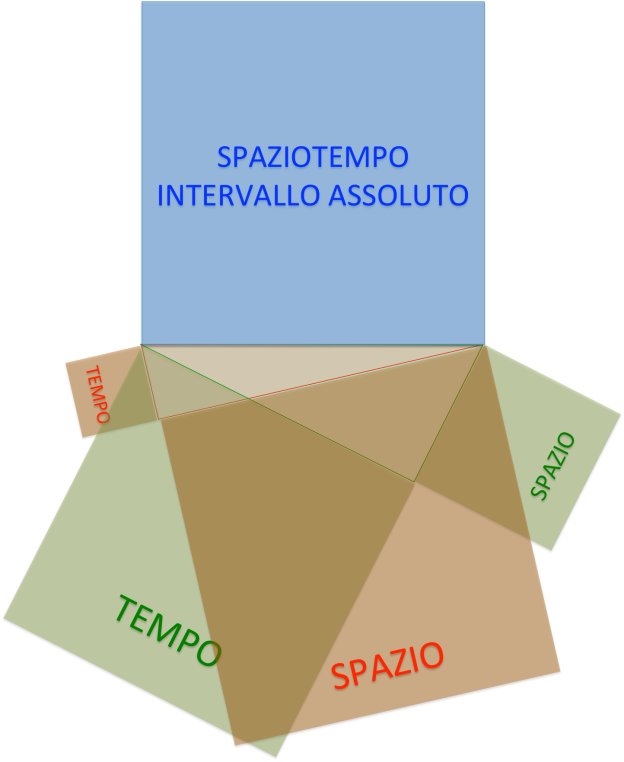
Per capire il parallelo, è necessario fare riferimento alle antiche conoscenze delle medie, quando ci hanno spiegato il teorema di Pitagora, secondo il quale il quadrato costruito sull’ipotenusa è uguale alla somma dei quadrati costruiti sui cateti. Il che significa che se “teniamo ferma” l’ipotenusa e facciamo variare i cateti, otteniamo infinite combinazioni di cateti la somma dei cui quadrati è uguale a quel quadrato che abbiamo “tenuto fermo”. E ora guardiamo la figura. Il quadrato sull’ipotenusa rappresenta il continuum spaziotemporale, uno dei cateti rappresenta lo spazio (o meglio il quadrato costruito su di esso) e il quadrato costruito sull’altro cateto rappresenta il tempo.

 

La parte azzurra del disegno rappresenta il continuum spaziotemporale, mentre la parte rossa e la parte verde sono due esempi di come rappresentare quel continuum. Nella parte verde la superficie occupata dal tempo è molto elevata, nella parte rossa è molto elevata la superficie occupata dallo spazio.

Quel che ci dice Einstein è che sia l’osservatore verde sia l’osservatore rosso vedono la stessa cosa, lo stesso continuum azzurro, semplicemente è rappresentato in due modi diversi. E allora, consentitemi di ripetere qui di seguito i versi di Blake.

Per vedere un mondo in un granello di sabbia,
E un paradiso in un fiore di campo,
Poni l’infinito nel palmo della mano
E l’eternità in un’ora.

E’ un po’ come la mela di Newton. Solo che la gravità non è una “forza”, ma una deformazione dello spaziotempo. Per cui quella mela può essere immaginata come la Terra, che ruota attorno al sole non perché c’è una forza che l’attrae, ma perché la curvatura dello spaziotempo la obbliga a muoversi su quella traiettoria. Una mela intelligente, insomma…

 

Il tempo è relativo

Il mio buon amico masticone, commentando il post su Einstein, mi ha detto che avrei dovuto fare il fisico. E questo ha riportato alla mia memoria un episodio, di quando ero appena laureato. Il mio prof di Fisica II mi cercò, e mi propose di fare il ricercatore. In realtà non era ancora professore, era l’assistente del professore. Erano i tempi in cui stava nascendo Tor Vergata, la seconda università di Roma, e un manipolo di validi assistenti aveva finalmente la possibilità di avere la cattedra. E lui si acchiappò la cattedra di Fisica II a Ingegneria, Io lo ammiravo tantissimo per il modo con cui insegnava, scanzonato ma rigoroso al tempo stesso, e anche per il suo nome, perché si chiama Folco, un nome che per me era un nome evocativo di mondi lontani e oceani inesplorati. La proposta mi tentava, e molto, ma fu lui stesso a dire una cosa che mi dissuase completamente. Mi disse che lui proveniva da famiglia ricca, e quindi poteva mantenere un tenore di vita decente nonostante lo stipendio universitario. E disse anche che se avesse dovuto vivere di quello, sarebbe stata veramente dura. Ho apprezzato molto l’onestà intellettuale, l’ho ringraziato moltissimo, e ho deciso di fare altro.

Ma evidentemente, come dice masticone, la passione per la scienza mi è rimasta nel sangue, e come gli ho detto rispondendo al suo commento, quello che mi ha sempre affascinato nello studio, e in particolare negli studi scientifici, come la matematica e la fisica, è la scoperta. La scoperta di cose che non so, il “vedere” cose che magari erano lì, sotto il mio naso, ma che non avrei mai pensato di osservare. Il “capire come funziona”. Ci sono cose che per essere comprese richiedono degli strumenti complessi. Matematica superiore, derivate parziali, trasformate di Fourier e di Laplace, e via discorrendo. Per cui di norma matematica e fisica vanno di pari passo. Quello che, lo ribadisco ancora una volta, mi ha invece affascinato della teoria della relatività ristretta di Einstein, è proprio l’esprimibilità dei concetti base senza ricorrere ad alcuno strumento matematico complesso. E addirittura, la possibilità di fare discorsi qualitativi, ma che fanno comprendere l’essenza della teoria.

E siccome una delle cose che mi piacciono tanto è condividere l’informazione, e credo di essere in grado di farlo in modo relativamente (ahah) chiaro, vorrei tentare di trasferire il concetto di relatività del tempo.

I fondamenti della teoria sono due: il primo è che se due persone si stanno muovendo una rispetto all’altra con un movimento rettilineo e a velocità costante, non è possibile stabilire chi sia fermo e chi si muove, e il secondo è che la velocità della luce è costante in qualunque sistema di riferimento. Questa seconda affermazione è meno banale di quanto possa apparire ma per ora non andiamo oltre.

Dovendo misurare il tempo, immaginiamo un orologio basato su un principio semplice. Due specchi posizionati ad una certa distanza tra di loro, con un raggio di luce che “rimbalza” dall’uno all’altro, indefinitamente, e supponiamo di avere un sistema per contare i rimbalzi. Non importa quanto sia complesso realizzarlo in pratica, ai fini del ragionamento. Ovviamente la luce si muove in linea retta, quindi se i due specchi sono paralleli il raggio di luce non “scapperà” fuori. Nella figura qui accanto c’è uno schemino che sintetizza questo dispositivo teorico.

Ora supponiamo di avere uno di questi orologi accanto a noi, e di darne uno al nostro amico Bob, e che Bob si trovi a bordo di un veicolo che si muove rispetto a noi in linea retta a velocità costante. Ad esempio, supponiamo di trovarci sul marciapiede di una stazione ferroviaria e che il nostro amico Bob sia su un treno che passa senza fermarsi.

Ora immaginiamo di scattare tre fotografie molto velocemente, in modo da fotografare l’orologio del nostro amico mentre il raggio di luce si sta muovendo da uno specchio all’altro. Se sovrapponiamo le tre foto otteniamo una cosa di questo tipo, dove non è ancora rappresentato il raggio di luce. Questo schema rappresenta l’orologio in movimento di Bob così come appare a noi che lo stiamo osservando da fermi.

Ora facciamo un semplice ragionamento. Supponiamo che siamo stati sufficientemente veloci a scattare da cogliere i momenti in cui il raggio di luce è rimbalzato sugli specchi, ciò significa che il percorso della luce che noi vediamo è rappresentato da questa figura.

È intuitivo che il percorso compiuto dalla luce è più lungo. Ma siccome inizialmente abbiamo postulato che la velocità della luce sia costante in qualsiasi sistema di riferimento, ciò significa semplicemente che se il percorso è più lungo, e la velocità è la stessa, allora il tempo deve essere maggiore. Che cosa significa tutto questo? Significa che il tempo di Bob, che io osservo, scorre più lentamente. Ed è per questo che il gemello che parte torna più giovane. Solo che questo effetto diventa misurabile quando le velocità iniziano ad essere comparabili con quella della luce. Per avere un’idea, la velocità della luce è di 300.000 chilometri al secondo, mentre un aereo di linea si muove a circa 200 metri al secondo…

Io credo che messa in questi termini la relatività sia comprensibile a chiunque. E’ evidente che ci sono anche altri aspetti, più complessi, che implicano la necessità di eseguire dei calcoli, eccetera. Ma. Ma intuitivamente, qualitativamente come si dice quando si parla di scienza, l’idea alla base della teoria brilla sfavillante nella sua evidenza, nella sua semplicità. Al punto da far scattare la domanda “ma perché non l’ho visto?”. Ecco, perché? Era lì. Aspettava solo di essere scoperta.

Giangius, che mi onora leggendomi e commentandomi, faceva notare come l’humus scientifico degli anni intorno al 1905 era favorevole per effettuare la scoperta. E io sono assolutamente d’accordo. Erano i tempi in cui si pensava che ci fosse il cosiddetto “etere”, il mezzo all’interno della quale la luce doveva propagarsi. Essendo la luce di natura ondulatoria, si riteneva avesse bisogno di un mezzo, l’etere per l’appunto, per potersi propagare. Michelson e Morley, una coppia di scienziati dell’epoca, misero in piedi un esperimento che, contrariamente alle aspettative, dimostrò che l’etere non esisteva.

Ma il mio punto è sempre lo stesso. E’ verissimo che l’humus era favorevole, ma è altrettanto vero che una rivoluzione di questo tipo è geniale. Soprattutto quando si pone in modo così semplice, lineare, ed evidente. Ecco, tutto qui.

Blog, fai il tuo mestiere

Caro blog, se sei un serbatoio di pensieri occasionali, vuol dire che da serbatoio ti devi comportare. E siccome sono alla ricerca spasmodica di un succedaneo della corsa, ti toccherà sopportare, e accogliere nella tua pancia dei pensieri sconclusionati qualunque.

Stamattina mi è venuta in mente la parola ordalia. Non mi ero mai imbattuto nella parola ordalia prima della lettura di Dune, di Frank Herbert. Dal libro fu tratto anche un film di Lynch, ma come spesso accade la resa cinematografica di un romanzo non è mai completamente all’altezza. E ricordo che incontrai la parola proprio all’inizio del romanzo, quando il giovane Paul Atreides ne subisce una da parte della Reverenda Madre.

– Bene – disse la vecchia, – hai superato la prima prova. E adesso, ecco in che cosa consiste la seconda: se togli la mano dalla scatola, muori. Nient’altro. Tieni la mano nella scatola, e vivi. Toglila, e muori. Paul respirò profondamente per calmare il tremito. – Se urlo, in un attimo la stanza sarà invasa dai servi, e allora voi morirete!
– I servi non passeranno oltre tua madre, che è di guardia fuori da questa portá. Puoi esserne certo. Tua madre ha superato questa prova. Ora è il tuo turno. Devi esserne onorato. Molto raramente sottoponiamo dei ragazzi ad essa.
La curiosità ridusse il terrore di Paul a un livello controllabile. Non poteva negarlo: le parole della vecchia gli erano suonate sincere. Se sua madre era di guardia fuori… se questa era veramente una prova… Qualsiasi cosa fosse, sapeva di esserci dentro fino al collo, intrappolato da quella mano con l’ago, il gom jabbar. Richiamò alla mente la litania contro la paura che sua madre gli aveva insegnato, secondo il rito Bene Gesserit.
Non devo aver paura. La paura uccide la mente. La paura è la piccola morte che porta con sé l’annullamento totale. Guarderò in faccia la mia paura. Permetterò che mi calpesti e mi attraversi. E quando sarà passata, aprirò il mio occhio interiore e ne scruterò il percorso. Là dove andrà la paura non ci sarà più nulla. Soltanto io ci sarò.
Sentì la calma invaderlo nuovamente, ed esclamò: – Sbrigatevi, vecchia.
– Vecchia! ribatté lei. – Hai del coraggio, non si può negare. Bene, vedremo, signor mio. – Si chinò su di lui, sfiorandolo, e abbassò la voce fino a un bisbiglio: – Sentirai dolore alla mano, nella scatola. Un dolore atroce, ma… Ritira la mano e ti toccherò il collo col gom jabbar! La sua morte è rapida come la scure che mozza il capo al condannato. Ritira la mano, e il gom jabbar ti ucciderà. Hai capito?
– Che cosa c’è nella scatola?
– Dolore.

Ecco. Questo è il senso dell’ordalia. Cosa c’è nella scatola? Dolore. Questo rappresenta la parola meglio di ogni spiegazione, meglio di ogni definizione. Una scatola vuota dove devi mettere una mano, e sai che ci sarà dolore. E non puoi sottrarti, altrimenti il gom jabbar penetrerà nella gola e ti ucciderà all’istante. Ordalìa. Ha un suono sinistro. Solo pronunciarla fa paura. Ma come dice il giovane Atreides, la paura va guardata in faccia, bisogna permetterle di attraversarci, per aprire il nostro occhio interiore e vedere da dove è passata. E dove andrà la paura, non ci sarà niente. Soltanto io ci sarò.

E la paura mi ha fatto venire in mente la fisica quantistica (e poi lo dico il collegamento, eh). C’è un filmato stupendo che illustra l’esperimento delle due fessure. Quello che fa capire come la particella possa essere in due posti nello stesso momento. E’ un cartone di pochi minuti

Ecco, il collegamento con la paura è quello finale, perché l’elettrone ha “paura” di essere osservato. E avendo paura, “decide” di fregare l’osservatore. Ma. Ma così si fa male da solo alla fine. Perché scegliendo, perde la seconda possibilità. Perde la possibilità di essere in due posti nello stesso momento. Ma alla fine non è neanche colpa del povero elettrone. E’ colpa dell’osservatore. Che vuol dire tutto questo? Boh.

Ma ho letto un interessante post di un blog che mi ha attirato innanzitutto per il nome. Il blog si chiama “Rem tene, verba sequentur”, che ha risvegliato in me delle reminiscenze antiche, quando facevo le versioni di latino ed ero uno dei pochi a cui il latino piacesse. E tacevo questo fatto, per non essere sbeffeggiato. Ma penetrare la frase latina era quasi come risolvere un’equazione, un procedimento molto molto logico. E la frase che dà il titolo al blog invita a stare sulle cose, perché nel momento in cui si conoscono le cose le parole verranno da sole. Questa frase, attribuita a Catone, rappresenta una rottura rispetto al credo aristotelico secondo cui è necessario sì conoscere, ma è necessario anche sapere come dire ciò che si conosce. In questo specifico, Catone è assai più intrigante, perché mette l’accento sull’esigenza conoscitiva, sull’approfondimento, sulla sostanza. E anche se è vero che la forma è sostanza, è anche vero che la sostanza può diventare forma. E comunque, siccome sto divagando come sempre, vorrei dire che il post cui mi riferisco è questo, e dice che se ti fai scappare una cosa l’hai persa, perché non si torna indietro. Come l’elettrone.

E chi è l’osservatore esterno che si prende la colpa? Difficile da capire, perché restiamo confinati a questo mondo. Mentre l’osservatore che disturba l’elettrone appartiene ad un altro mondo. C’è un osservatore lì fuori? Che forma ha? Siamo come le figure piane di Flatland che non conoscono la terza dimensione? Che non conoscono il volume? Esiste una quarta dimensione? Esiste l’entanglement? Quella teoria secondo la quale siccome all’inizio dei tempi, nel momento del Big Bang, era tutto unito, allora le cose sono effettivamente tutte legate, e la distanza tra particelle è un di cui? E se io prendo due elettroni appartenenti allo stesso atomo, ne porto uno a distanza ragguardevole, e lo stimolo, l’altro risponde. Ecco questo entanglement, ha applicazioni pratiche nel macromondo? Esistono comunicazioni extrasensoriali?

E che ne so? Così risponderebbe Quelo. Sai a che ora me so’ alzato stamattina? Alle 7 meno un quarto, e la bambina mi ha vomitato in macchina.